Standard conjectures on algebraic cycles

In mathematics, the standard conjectures about algebraic cycles is a package of several conjectures describing the relationship of algebraic cycles and Weil cohomology theories. One of the original applications of these conjectures, envisaged by Alexander Grothendieck, was to prove that his construction of pure motives gave an abelian category that is semisimple. Moreover, as he pointed out, the standard conjectures also imply the hardest part of the Weil conjectures, namely the "Riemann hypothesis" conjecture that remained open at the end of the 1960s and was proved later by Pierre Deligne; for details on the link between Weil and standard conjectures, see Kleiman (1968). The standard conjectures remain open problems, so that their application gives only conditional proofs of results. In quite a few cases, including that of the Weil conjectures, other methods have been found to prove such results unconditionally.

The classical formulations of the standard conjectures involve a fixed Weil cohomology theory H. All of the conjectures deal with "algebraic" cohomology classes, which means a morphism on the cohomology of a smooth projective variety

H*(X) → H*(X)

induced by an algebraic cycle with rational coefficients on the product X × X via the cycle class map (which is part of the structure of a Weil cohomology theory).

Contents

Lefschetz type standard conjecture

Lefschetz type standard conjecture, also called conjecture B: One of the axioms of a Weil theory is the so-called hard Lefschetz theorem (or axiom): for a fixed smooth hyperplane section

W = H ∩ X,

for H some hyperplane in the ambient projective space PN containing the given smooth projective variety X, the Lefschetz operator

L : Hi(X) → Hi+2,

which is defined by intersecting cohomology classes with W gives an isomorphism

Ln-i: Hi(X) → H2n-i(X) (i ≦ n = dim X).

Define

Λ : Hi(X) → Hi-2(X) for 'i ≦ n

be the composition

(Ln-i+2)-1 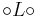\circ L \circ (Ln-i)-1

and

Λ : H2n-i+2(X) → H2n-i(X)

by

(Ln-i) 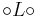\circ L \circ (Ln-i+2)-1 -1.

The Lefschetz conjecture states that the Lefschetz operator Λ is induced by an algebraic cycle.

Künneth type standard conjecture

The Lefschetz conjecture implies the Künneth type standard conjecture, also called conjecture C: It is conjectured that the projectors H∗(X) ↠ Hi(X) ↣ H∗(X) are algebraic, i.e. induced by a cycle πi ⊂ X × X with rational coefficients. This implies that every pure motive M decomposes in graded pieces of pure weights (see motives). The conjecture is known to hold for curves, surfaces and abelian varieties.

Conjecture D (numerical equivalence vs. homological equivalence)

Conjecture D states that numerical equivalence and homological equivalence agree. (It implies in particular the latter does not depend on the choice of the Weil cohomology theory). This conjecture implies the Lefschetz conjecture. If the Hodge standard conjecture holds, then the Lefschetz conjecture and Conjecture D are equivalent.

The Hodge standard conjecture

The Hodge standard conjecture is modelled on the Hodge index theorem. It states the positive definiteness of the cup product pairing on primitive algebraic cohomology classes. If it holds, then the Lefschetz conjecture implies Conjecture D. In characteristic zero the Hodge standard conjecture holds, being a consequence of Hodge theory. In positive characteristic the Hodge standard conjecture is known only for surfaces and abelian varieties.

The Hodge standard conjecture is not to be confused with the Hodge conjecture which states that for smooth projective varieties over C, every rational (p,p)-class is algebraic. The Hodge conjecture implies the Lefschetz conjecture and conjecture D for varieties over fields of characteristic zero. Likewise for fields of finite characteristic the Tate conjectures in ℓ-adic cohomology imply the Lefschetz conjecture.

References